|
Einführung
Die meisten natürlichen und in der Technik verwendeten festen Materialien liegen in kristalliner Form mit polykristallinem Aufbau vor oder sind zumindest teilkristallin. Ihr Gefüge wird gekennzeichnet durch die Phasen-, Korn- und Substruktur sowie durch die Textur, d.h. die Verteilung der kristallographischen Orientierungen. Die Kristallstruktur der Kristallite bewirkt die Anisotropie einer Reihe technisch wichtiger Materialeigenschaften. Treten
in einem polykristallinen Werkstück bestimmte Orientierungen der Kristallite bevorzugt auf, dann wird - auch bei einer Mittelung über eine sehr große Anzahl von Kristalliten - in der Regel eine gewisse Anisotropie übrigbleiben. Die makroskopischen Materialeigenschaften polykristalliner Materialien hängen also nicht nur von der Größe, Form und Anordnung der Kristallite ab, sondern auch ganz wesentlich von ihrer Textur. Das Mikrogefüge, die Art der Korngrenzen und die Textur
sind der Schlüssel zur Beschreibung der Anisotropie polykristalliner Stoffe.
Da technische Prozesse wie das Walzen, Gießen, Strangpressen oder eine Wärmebehandlung die Orientierungsverteilung in einem Werkstück in charakteristischer Weise ändern, kommt in der industriellen Fertigung der Textur als Werkstoffparameter eine besondere Bedeutung zu. Daneben ist die Entwicklung von Werkstoffen mit maßgeschneiderter Textur von Interesse, bei denen die anisotropen Eigenschaften eines vorzugsorientierten Werkstückes
dem jeweiligen Einsatzprofil angepasst werden. Auch in der Forschung ist die Texturanalyse zu einem Hilfsmittel bei der Untersuchung von Vorgängen geworden, die mit Änderungen des kristallinen Aufbaus verbunden sind.
Ein wichtiger Aspekt in der aktuellen Texturforschung ist die Weiterentwicklung experimenteller Methoden, um die Orientierungsverteilung in einem polykristallinen Material möglichst genau zu bestimmen. Der Messung der lokalen Textur im Mikrobereich kommt hierbei besondere Bedeutung zu, weil Werkstoffe oftmals eine inhomogene Textur zeigen, d.h. die Textur von der betrachteten Probenstelle abhängt. Die Kenntnis von Texturinhomogenitäten ist
wichtig, da sie mit lokalen Unterschieden in den Werkstoffeigenschaften verbunden sind.
EBSD-Grundlagen
|
|
 Die Kikuchi-Beugung in Rückstreuung von massiven Kristall- oberflächen ist eine sehr alte Technik [1], sie hat aber erst seit wenigen Jahren unter der Bezeichnung EBSD (Electron BackScatter Diffraction) eine breite Anwendung in den Werkstoff- und Erdwissenschaften
gefunden
[2, 3]. Wenn
ein Elektronenstrahl von einigen tausend Elektronenvolt Energie auf einen Kristall trifft, entsteht ein Beugungsdiagramm (a). Die Kikuchi-Beugung in Rückstreuung von massiven Kristall- oberflächen ist eine sehr alte Technik [1], sie hat aber erst seit wenigen Jahren unter der Bezeichnung EBSD (Electron BackScatter Diffraction) eine breite Anwendung in den Werkstoff- und Erdwissenschaften
gefunden
[2, 3]. Wenn
ein Elektronenstrahl von einigen tausend Elektronenvolt Energie auf einen Kristall trifft, entsteht ein Beugungsdiagramm (a).
Typisch für Kikuchi-Diagramme sind schmale Bänder mit einer Winkelbreite des doppelten Braggwinkels (b). Man kann sie sich anschaulich als Schnittlinien der Kosselkegel mit der Registrierebene vorstellen. Die Netzebenen würden in diesem Bild bis zum Leuchtschirm reichen und die Mittellinien der Bänder bilden. Die Bänder schneiden sich in sternförmigen Zonenachsen. Wegen der starken Vorwärtsstreuung
liegt das Intensitätsmaximum nahe
dem Maximum
im Fall von lichtoptischer Reflexion. Um eine ausreichend hohe Intensität zu erhalten, wird im Raster-Elektronenmikroskop (REM) die Probenoberfläche um etwa 60° bis 70° aus der Horizontalen gekippt und das Beugungsdiagramm mit einem Durchsicht-Leuchtschirm registriert. Dahinter steht eine hochempfindliche Digital-Videokamera. Das Beugungsdiagramm umfasst einen Winkelbereich von bis zu etwa ±60°, so dass meist mehrere niedrig indizierte Zonenachsen registriert werden.
Auf meiner Webseite www.ebsd.info finden Sie auf Englisch eine umfangreiche Einführung in das Arbeitsgebiet.
|
|
|
Nachdem mehrere Bänder im Diagramm mittels Radon- bzw. Hough- Transformation [3] lokalisiert wurden, erfolgt die Berechnung der Kristallorientierung durch Vergleich der Diagrammgeometrie mit der Position von Netzebenen in der Elementarzelle des Kristalls. Das Rechenprogramm versucht in einem mehrphasigen Material, das Diagramm mit allen vermuteten Kristallgittern zu indizieren und nimmt diejenige
Lösung
als wahr an, für die das
rückgerechnete (theoretische) Diagramm am besten mit dem gemess
enen Diagramm übereinstimmt ("Phasendiskriminierung").
Aus der Indizierung folgt die Kristallorientierung bezüglich des probenfesten Koordinatensystems in Form von Eulerwinkeln oder Miller-Indizes. In weiteren Programmen werden die gemessenen Orientierungsdaten analysiert. Die Verteilung der Kornorientierung im gemessenen Probenbereich wird in Gefügebildern veranschaulicht, indem den
Orientierungen in den Messorten Farben zugeordnet werden, die spezifisch
für die Miller-Indizes,
die Eulerwinkel oder die Rodrigues-Vektoren sind ("Miller Maps" =
"Inverse Polefigure Maps", "Euler-Maps", "Rodrigues-Maps") [4].
Die quantitative Texturanalyse erfolgt durch Berechnen der Orientierungs-Dichte-Funktion (ODF), Missorientierungs- und Orientierungs- Korrelationsfunktionen (MODF) sowie Konstruktion von Polfiguren. Die Orientierungsstereologie zielt ab auf die Verbindung von Textur und Quantitativer Materialographie, zum Beispiel die
Ermittlung von Korn- und Korngrenzen-Statistiken und von lokalen anisotropen Materialeigenschaften.
Insgesamt ermöglicht
EBSD eine umfangreiche quantitative Gefügecharakterisierung über den
gesamten gemessenen Bereich mit einer hohen Ortsauflösung bis herab auf
wenige 10 nm und einer Orientierungsgenauigkeit von typischerweise 0,5°
[5].
|
|
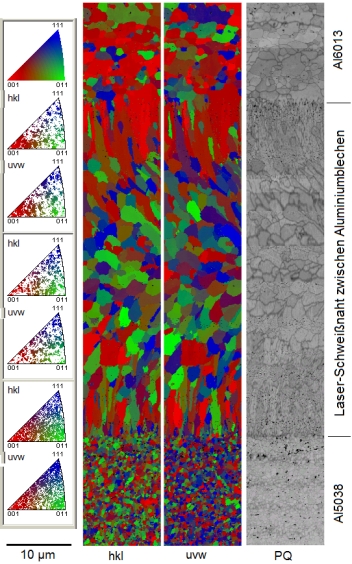
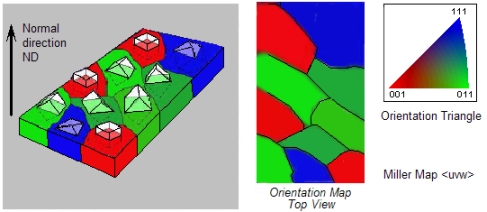 Die Farbcodierung der hkl- und der uvw- Richtungsverteilungsbilder ("Miller Maps") wird üblicherweise durch Überlagerung des RGB-Farbdreiecks mit dem Standard-Dreieck des Kristallgitters definiert [4]. Wegen der starken Verzerrung infolge der stereographischen Projektion
ist
die
Identifikation einer
kristallographischen
Richtung durch Vergleich der Farbe eines Korns mit der Farbe im Standarddreieck nicht immer einfach. Werden dagegen dieauf Summe = 1 normierten Indizes [100], [010] und [001] - wie die Elemente einer ternären Legierung in Phasendiagrammen - als Eckpunkte in ein gleichseitiges Dreieck eingetragen und die RGB-Farben mit baryzentrischer Gewichtung gemischt, dann ergibt sich ein einfacher linearer Zusammenhang zwischen den Orten der RGB-Mischfarben und den Orten der Flächenindizes [hkl] bzw. den Richtungsindizes
[uvw]. Für die Farbkodierung in Miller-Maps wird im Fall kubischer Symmetrie das intensiv dargestellte Farbdreieck
100-110-111 verwendet, das alle kristallographisch äquivalente Richtungen
enthält. Die Farbcodierung der hkl- und der uvw- Richtungsverteilungsbilder ("Miller Maps") wird üblicherweise durch Überlagerung des RGB-Farbdreiecks mit dem Standard-Dreieck des Kristallgitters definiert [4]. Wegen der starken Verzerrung infolge der stereographischen Projektion
ist
die
Identifikation einer
kristallographischen
Richtung durch Vergleich der Farbe eines Korns mit der Farbe im Standarddreieck nicht immer einfach. Werden dagegen dieauf Summe = 1 normierten Indizes [100], [010] und [001] - wie die Elemente einer ternären Legierung in Phasendiagrammen - als Eckpunkte in ein gleichseitiges Dreieck eingetragen und die RGB-Farben mit baryzentrischer Gewichtung gemischt, dann ergibt sich ein einfacher linearer Zusammenhang zwischen den Orten der RGB-Mischfarben und den Orten der Flächenindizes [hkl] bzw. den Richtungsindizes
[uvw]. Für die Farbkodierung in Miller-Maps wird im Fall kubischer Symmetrie das intensiv dargestellte Farbdreieck
100-110-111 verwendet, das alle kristallographisch äquivalente Richtungen
enthält.
|
|
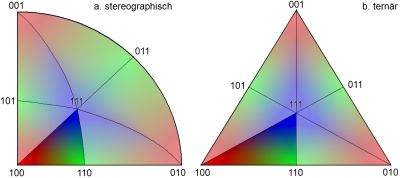 Ebenso kann man die Indizes [hkl] bzw. [uvw] von probenfesten Referenzrichtungen - bei Blechen wählt man in der Regel die Blechebenennormale und die Walzrichtung - auf Summe = 1 normieren und diese Werte für alle gemessenen Kristallite in ein ternäres Dreieck mit baryzentrischem Koordinatensystem eintragen
[6]. Man erhält so anstelle von inversen
Polfiguren eine neue Darstellung der statistischen Richtungsverteilungen bezüglich der
probenfesten Referenzrichtungen. Vorteile dieser Darstellungsart sind: Sie ist nicht verzerrt; die Indizes lassen sich mühelos ablesen; Indizes der Netzebenen mit gemeinsamer Zonenachse bzw. Indizes der Zonenachsen mit gemeinsamer Netzebene liegen auf Geraden. Aus historischen Gründen hat sich jedoch die Darstellung von ternären Millerplots noch nicht gegen die Darstellung von inversen Polfiguren mit der verzerrenden stereographischen oder Lambert-Projektion des kristallographischen Standard-Dreiecks
durchgesetzt. Ebenso kann man die Indizes [hkl] bzw. [uvw] von probenfesten Referenzrichtungen - bei Blechen wählt man in der Regel die Blechebenennormale und die Walzrichtung - auf Summe = 1 normieren und diese Werte für alle gemessenen Kristallite in ein ternäres Dreieck mit baryzentrischem Koordinatensystem eintragen
[6]. Man erhält so anstelle von inversen
Polfiguren eine neue Darstellung der statistischen Richtungsverteilungen bezüglich der
probenfesten Referenzrichtungen. Vorteile dieser Darstellungsart sind: Sie ist nicht verzerrt; die Indizes lassen sich mühelos ablesen; Indizes der Netzebenen mit gemeinsamer Zonenachse bzw. Indizes der Zonenachsen mit gemeinsamer Netzebene liegen auf Geraden. Aus historischen Gründen hat sich jedoch die Darstellung von ternären Millerplots noch nicht gegen die Darstellung von inversen Polfiguren mit der verzerrenden stereographischen oder Lambert-Projektion des kristallographischen Standard-Dreiecks
durchgesetzt.
|
|
___________
[1] Download S. Nishikawa, S. Kikuchi: Diffraction of cathode rays by calcite. Nature 1928, 122, 726
[2] A.J. Schwartz, M. Kumar, B.L. Adams (eds.): Electron Backscatter Diffraction in Materials Science. Kluwer Academic/Plenum
Press, New York, 2000.
[3] A.J. Schwartz, M. Kumar, B.L. Adams, D.P. Field (eds.): Electron Backscatter Diffraction in Materials Science.
Springer Science and Business Media, New York, 2009.
[4] Download D. Gerth und R.A. Schwarzer: Graphical representation of grain and hillock orientations in
annealed Al-1%Si films. Textures and Microstructures 21 (1993) 177-193.
[5] Download R.A. Schwarzer, D.P. Field, B.L. Adams, M. Kumar, A J. Schwartz: Present state of electron
backscatter diffraction and prospective developments. In: Adam J.
Schwartz, M. Kumar, Brent L. Adams, David P. Field (eds.): Electron
Backscatter Diffraction in Materials Science, 2nd edition, Springer
Science+Business Media, 2009, Chapter 1, p. 1-20.
[6] W.G. Fricke Jr.: Zone Axes in the Miller Index Space. Mat. Sci. Eng. 84 (1986) 205-208.
|
|
|

 Die Kikuchi-Beugung in Rückstreuung von massiven Kristall- oberflächen ist eine sehr alte Technik [1], sie hat aber erst seit wenigen Jahren unter der Bezeichnung EBSD (Electron BackScatter Diffraction) eine breite Anwendung in den Werkstoff- und Erdwissenschaften
gefunden
[2, 3]. Wenn
ein Elektronenstrahl von einigen tausend Elektronenvolt Energie auf einen Kristall trifft, entsteht ein Beugungsdiagramm (a).
Die Kikuchi-Beugung in Rückstreuung von massiven Kristall- oberflächen ist eine sehr alte Technik [1], sie hat aber erst seit wenigen Jahren unter der Bezeichnung EBSD (Electron BackScatter Diffraction) eine breite Anwendung in den Werkstoff- und Erdwissenschaften
gefunden
[2, 3]. Wenn
ein Elektronenstrahl von einigen tausend Elektronenvolt Energie auf einen Kristall trifft, entsteht ein Beugungsdiagramm (a). 
 Die Farbcodierung der hkl- und der uvw- Richtungsverteilungsbilder ("Miller Maps") wird üblicherweise durch Überlagerung des RGB-Farbdreiecks mit dem Standard-Dreieck des Kristallgitters definiert [4]. Wegen der starken Verzerrung infolge der stereographischen Projektion
ist
die
Identifikation einer
kristallographischen
Richtung durch Vergleich der Farbe eines Korns mit der Farbe im Standarddreieck nicht immer einfach. Werden dagegen dieauf Summe = 1 normierten Indizes [100], [010] und [001] - wie die Elemente einer ternären Legierung in Phasendiagrammen - als Eckpunkte in ein gleichseitiges Dreieck eingetragen und die RGB-Farben mit baryzentrischer Gewichtung gemischt, dann ergibt sich ein einfacher linearer Zusammenhang zwischen den Orten der RGB-Mischfarben und den Orten der Flächenindizes [hkl] bzw. den Richtungsindizes
[uvw]. Für die Farbkodierung in Miller-Maps wird im Fall kubischer Symmetrie das intensiv dargestellte Farbdreieck
100-110-111 verwendet, das alle kristallographisch äquivalente Richtungen
enthält.
Die Farbcodierung der hkl- und der uvw- Richtungsverteilungsbilder ("Miller Maps") wird üblicherweise durch Überlagerung des RGB-Farbdreiecks mit dem Standard-Dreieck des Kristallgitters definiert [4]. Wegen der starken Verzerrung infolge der stereographischen Projektion
ist
die
Identifikation einer
kristallographischen
Richtung durch Vergleich der Farbe eines Korns mit der Farbe im Standarddreieck nicht immer einfach. Werden dagegen dieauf Summe = 1 normierten Indizes [100], [010] und [001] - wie die Elemente einer ternären Legierung in Phasendiagrammen - als Eckpunkte in ein gleichseitiges Dreieck eingetragen und die RGB-Farben mit baryzentrischer Gewichtung gemischt, dann ergibt sich ein einfacher linearer Zusammenhang zwischen den Orten der RGB-Mischfarben und den Orten der Flächenindizes [hkl] bzw. den Richtungsindizes
[uvw]. Für die Farbkodierung in Miller-Maps wird im Fall kubischer Symmetrie das intensiv dargestellte Farbdreieck
100-110-111 verwendet, das alle kristallographisch äquivalente Richtungen
enthält.
 Ebenso kann man die Indizes [hkl] bzw. [uvw] von probenfesten Referenzrichtungen - bei Blechen wählt man in der Regel die Blechebenennormale und die Walzrichtung - auf Summe = 1 normieren und diese Werte für alle gemessenen Kristallite in ein ternäres Dreieck mit baryzentrischem Koordinatensystem eintragen
[6]. Man erhält so anstelle von inversen
Polfiguren eine neue Darstellung der statistischen Richtungsverteilungen bezüglich der
probenfesten Referenzrichtungen. Vorteile dieser Darstellungsart sind: Sie ist nicht verzerrt; die Indizes lassen sich mühelos ablesen; Indizes der Netzebenen mit gemeinsamer Zonenachse bzw. Indizes der Zonenachsen mit gemeinsamer Netzebene liegen auf Geraden. Aus historischen Gründen hat sich jedoch die Darstellung von ternären Millerplots noch nicht gegen die Darstellung von inversen Polfiguren mit der verzerrenden stereographischen oder Lambert-Projektion des kristallographischen Standard-Dreiecks
durchgesetzt.
Ebenso kann man die Indizes [hkl] bzw. [uvw] von probenfesten Referenzrichtungen - bei Blechen wählt man in der Regel die Blechebenennormale und die Walzrichtung - auf Summe = 1 normieren und diese Werte für alle gemessenen Kristallite in ein ternäres Dreieck mit baryzentrischem Koordinatensystem eintragen
[6]. Man erhält so anstelle von inversen
Polfiguren eine neue Darstellung der statistischen Richtungsverteilungen bezüglich der
probenfesten Referenzrichtungen. Vorteile dieser Darstellungsart sind: Sie ist nicht verzerrt; die Indizes lassen sich mühelos ablesen; Indizes der Netzebenen mit gemeinsamer Zonenachse bzw. Indizes der Zonenachsen mit gemeinsamer Netzebene liegen auf Geraden. Aus historischen Gründen hat sich jedoch die Darstellung von ternären Millerplots noch nicht gegen die Darstellung von inversen Polfiguren mit der verzerrenden stereographischen oder Lambert-Projektion des kristallographischen Standard-Dreiecks
durchgesetzt.